Ring of circles

I found a good mathematical resource for OpenGL from Cambridge University:

https://www.cl.cam.ac.uk/teaching/1718/AdvGraph/Printable%20(1-up).pdf

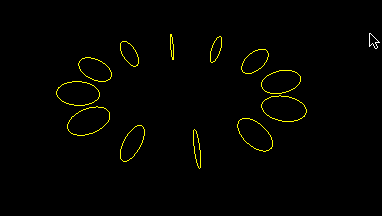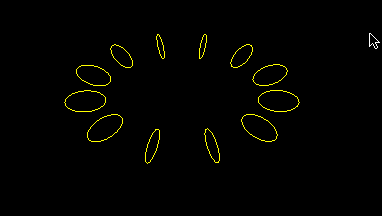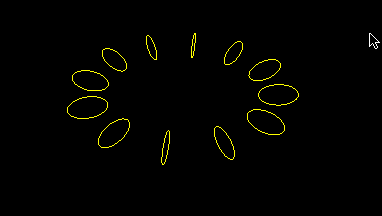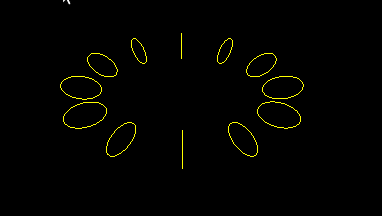
This is a simplified version of earlier program, hopefully to reduce unnecessary clutter:

https://gist.github.com/tthtlc/3ee685f66a6addc4082fde0a65b860fa

And instead of a circle, which is drawn as a polygon of 30 sides, we can fixed it to TWO-gon:

The rod-shaped structure formed a flat surface - with top and bottom surface. 

How to make it into a Mobius surface?   So what if now the generator of the 2gon is shifted by a angle offset as it goes round the circle - and the total angular offset should total 180 degrees?

This is the result:

And the source code is here:

https://gist.github.com/tthtlc/9db1b5a9609932a75f70f0d347b62228


Instead of a 2-gon, why not change it to a 3-gon (triangle) and you will get this:

Instead of triangle (ngon=3) or circle earlier (ngon=30), what if we want to form helix?   Then instead of drawing circle by itself, we need to rotate the circle while drawing the circle, forming this:

And the source code is here:

https://gist.github.com/tthtlc/43294d2f4346d5da834ad6aa6278dd13

And what if you make the circles move in a sinusoidal pattern around at the periodic frequency of 2?

The above is the result:

https://gist.github.com/tthtlc/5cc6268e7e8aa0f0025405557951f890

And in case you think the single colored rings are too boring:

https://gist.github.com/tthtlc/7245d5b53513fe13966eca1758921826

https://gist.github.com/tthtlc/d53c71446e58d9b09978aa1fc7e94e76