Sep 1, 2019
Euler Disc and its mathematics
As described in wikipedia:
Here are the videos where the Euler discs phenomenon is highlighted and explained:
https://www.youtube.com/watch?v=55gJgCoDld4 (interesting study of the Euler Disc motion from an engineering point of view).
https://www.real-world-physics-problems.com/eulers-disk.html (here the mathematics is worked out in details - and quite easy to understand with undergraduate Physics as background)
https://www.techly.com.au/2015/09/28/eulers-disk-amazing-plastic-disk-will-melt-brain-hear/
https://www.real-world-physics-problems.com/eulers-disk.html (here the mathematics is worked out in details - and quite easy to understand with undergraduate Physics as background)
https://www.techly.com.au/2015/09/28/eulers-disk-amazing-plastic-disk-will-melt-brain-hear/
Aug 18, 2019
Mathematical Optimal Control Theory
https://math.berkeley.edu/~evans/control.course.pdf
Bellman Optimality Principle:
Markov property of stochastic processes:
Optimal Value Function:
Computing the optimal action:
Bellman Equations:
Aug 12, 2019
Exploring about Mandelbrot Set
https://www.youtube.com/watch?v=FFftmWSzgmk
And trying out the GeoGebra software:
https://www.geogebra.org/m/BUVhcRSv (these files are from Ben)
To see the sequence of square operation and its path:
Jul 7, 2019
Jul 3, 2019
Jun 30, 2019
Ring of circles
I found a good mathematical resource for OpenGL from Cambridge University:
https://www.cl.cam.ac.uk/teaching/1718/AdvGraph/Printable%20(1-up).pdf
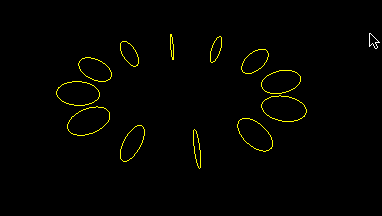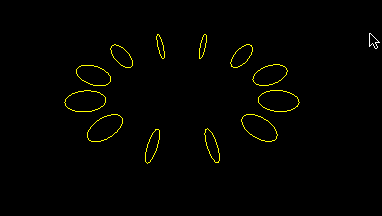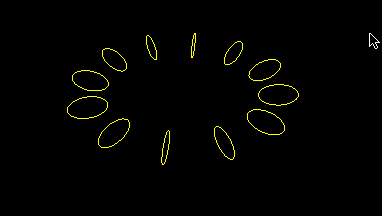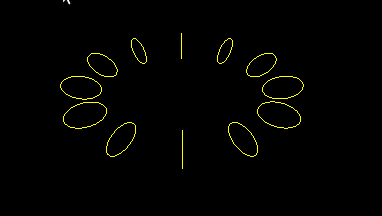
This is a simplified version of earlier program, hopefully to reduce unnecessary clutter:
https://gist.github.com/tthtlc/3ee685f66a6addc4082fde0a65b860fa
And instead of a circle, which is drawn as a polygon of 30 sides, we can fixed it to TWO-gon:
And instead of a circle, which is drawn as a polygon of 30 sides, we can fixed it to TWO-gon:
The rod-shaped structure formed a flat surface - with top and bottom surface.
How to make it into a Mobius surface? So what if now the generator of the 2gon is shifted by a angle offset as it goes round the circle - and the total angular offset should total 180 degrees?
This is the result:
And the source code is here:
https://gist.github.com/tthtlc/9db1b5a9609932a75f70f0d347b62228
Instead of a 2-gon, why not change it to a 3-gon (triangle) and you will get this:
And the source code is here:
https://gist.github.com/tthtlc/43294d2f4346d5da834ad6aa6278dd13
And what if you make the circles move in a sinusoidal pattern around at the periodic frequency of 2?
The above is the result:
https://gist.github.com/tthtlc/5cc6268e7e8aa0f0025405557951f890
And in case you think the single colored rings are too boring:
https://gist.github.com/tthtlc/7245d5b53513fe13966eca1758921826
How to make it into a Mobius surface? So what if now the generator of the 2gon is shifted by a angle offset as it goes round the circle - and the total angular offset should total 180 degrees?
This is the result:
And the source code is here:
https://gist.github.com/tthtlc/9db1b5a9609932a75f70f0d347b62228
Instead of a 2-gon, why not change it to a 3-gon (triangle) and you will get this:
Instead of triangle (ngon=3) or circle earlier (ngon=30), what if we want to form helix? Then instead of drawing circle by itself, we need to rotate the circle while drawing the circle, forming this:
https://gist.github.com/tthtlc/43294d2f4346d5da834ad6aa6278dd13
And what if you make the circles move in a sinusoidal pattern around at the periodic frequency of 2?
The above is the result:
https://gist.github.com/tthtlc/5cc6268e7e8aa0f0025405557951f890
And in case you think the single colored rings are too boring:
https://gist.github.com/tthtlc/7245d5b53513fe13966eca1758921826
Jun 29, 2019
Jun 28, 2019
Creating a torus (animated and variations)
Looking at the Pentagon torus:
And its source code:
And changing the rings to 30:
And if you use triangle surface to create the Pentagonal torus in 3D:
What are the difference in programming? In the previous two, the torus is created by a prebuilt function called (look into the "display()" function for how the object is generated) glutWireTorus().
global xrot, yrot, zrotBut in the case of triangulated surface generated torus it is built from scratch using "triangle", and thus can be controlled via use of cosine() and sine() to generate the triangles for the surface of the torus. The technique is to generate a list of coordinates of the vertices of the surface, and the normal vector centering on that coordinate.
global ndisc
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
glLoadIdentity()
gluLookAt(
0.0, 0.0, 10.0,
0.0, 0.0, 0.0,
0.0, 1.0, 0.0)
glRotatef(xrot, 1.0, 0.0, 0.0)
glRotatef(yrot, 0.0, 1.0, 0.0)
glRotatef(zrot, 0.0, 0.0, 1.0)
glColor3f(0.5, 0.0, 1.0)
glutWireTorus(0.5,1.5,5,5)
glFlush()
glutSwapBuffers()
vertices = []
normals = []
u_step = 2 * pi / (slices)
v_step = 2 * pi / (inner_slices)
u = 0.
for i in range(slices+1):
cos_u = cos(1*u)
sin_u = sin(1*u)
v = 0.
for j in range(inner_slices):
cos_v = cos(1*v)
sin_v = sin(1*v)
d = (radius + inner_radius * cos_v)
x = d * (cos_u +2)* cos_u
y = d * (cos_u +2)* sin_u
z = inner_radius * sin_v
nx = cos_u * cos_v
ny = sin_u * cos_v
nz = sin_v
vertices.extend([x, y, z])
normals.extend([nx, ny, nz])
v += v_step
u += u_step
# Create a list of triangle indices.
indices = []
for i in range(slices):
for j in range(inner_slices):
p = i * inner_slices + j
indices.extend([p, p + inner_slices, p + inner_slices + 1])
indices.extend([p, p + inner_slices + 1, p + 1])
self.vertex_list = batch.add_indexed(len(vertices)//3,
GL_TRIANGLE_STRIP,
group,
indices,
('v3f/static', vertices),
('n3f/static', normals))
May 16, 2019
Riemann Hypothesis
https://www.youtube.com/watch?v=VTveQ1ndH1c
How mpmath implemented Zeta Function:
Another implementation:
Study of primes:
Mar 22, 2019
Mar 2, 2019
The Schrödinger Equation for the Hydrogen Atom: A generalization
This is a two-body problem (diatomic molecule) and formulation of the problem is possible:
And its solution is using Spherical Harmonics:
http://mathworld.wolfram.com/SphericalHarmonic.html
So how about 3-body, or n-body system?
How complexity creeps in arising from n-bodies to n-1 bodies interaction?
https://www.youtube.com/watch?v=09iTidqkriw (very good video on the history)
and the github for the codes mentioned above is here:
https://github.com/winsmith/n-body-problem
and the github for the codes mentioned above is here:
https://github.com/winsmith/n-body-problem
Complex, but simulation is possible:
Feb 12, 2019
Jan 3, 2019
Jan 2, 2019
Category Theory: its concepts and applications
https://www.cl.cam.ac.uk/teaching/1819/L108/
Less abstract:
Types reasoning:
Category Theory Applied to Functional Programming
Categories for the working Hackers:
Subscribe to:
Posts (Atom)


























